📚 Volta às aulas com até 10% de desconto + 5% no PIX! 💎 + Cupom! 🏷️
R$ 59,90 O preço original era: R$ 59,90.R$ 54,90O preço atual é: R$ 54,90.
Métodos de Pagamento:

DISCIPLINA: CÁLCULO INTEGRAL
TEMA: Volume de sólidos de revolução.
OBJETIVO: Verificar a teoria e prática do conteúdo sólidos de revolução.
COMPETÊNCIA: Calcular o volume de sólidos de revolução através fórmula contendo integrais.
EXPERIMENTE E PRODUZA:
Muitos sólidos são possíveis de se calcular com o uso de fórmulas simples tais como o volume de paralelepípedo, prisma, pirâmide, cilindro, cone e esfera. Abaixo temos a figuras e suas fórmulas.
Paralelepípedo
𝑉 = 𝑎 ⋅ 𝑏 ⋅ 𝑐
Prisma
𝑉 = 𝐴𝑏 ⋅ ℎ
𝐴𝑏: área da base
Pirâmide
𝑉 = 𝐴𝑏 ⋅ ℎ
3
Cilindro
𝑉 = 𝜋 ⋅ 𝑟2 ⋅ ℎ
Cone
𝑉 = 𝜋 ⋅ 𝑟2 ⋅ ℎ
3
Esfera
𝑉 = 4
3 𝜋 ⋅ 𝑟3
Porém outras figuras os cálculos dos volumes não são tão imediatos. É preciso de cálculos mais avançados tais como o cálculo integral.
“No estudo da geometria espacial, os sólidos geométricos se originam da rotação 360 de uma figura plana em torno de um eixo principal determinado por uma reta. O sólido de revolução é obtido pelo giro de uma região plana limitada e descrita em torno de um eixo central, chamado também de eixo de revolução.” (RODRIGUES, p. 15)
Para calcular volume gerado pela revolução da curva em torno do eixo x é necessário aplicar é dado por 𝑉 = 𝜋 ∫ [𝑓(𝑥)]2𝑑𝑥𝑏𝑎 .
Agora é com você!
Para que você aplique a uma situação prática este conteúdo queremos que você calcule o volume de um objeto de sua casa. Minha sugestão é que seja um balde com formato em tronco de cone (não é permitido utilizar o formato de um cilindro). Mas pode ser outro objeto, desde que consiga obter a função 𝑦 = 𝑓(𝑥). Observe os passos a seguir:
1) Meça a altura do balde e o diâmetro de suas duas bases (conforme fotos).
2) Com base nos dados obtidos modele a função 𝑦 = 𝑓(𝑥). Com os dados obtidos o professor conseguiu a figura abaixo. Pode-se observar que a função é linear, o coeficiente linear visível no gráfico e o coeficiente linear também está fácil de calcular (dica: trace uma reta horizontal no eixo y quando inicia a reta inclinada. Com o triângulo retângulo obtido calcule Δ𝑥Δ𝑦).
3) Calcule o volume do sólido de revolução.
4) Os valores obtidos na etapa 3 provavelmente serão em centímetros cúbicos. Transforme para litros.
5) Com um becker ou uma garrafa pet de 1 litro (ou 1,5 litros ou 2,5 litros etc) meça seu objeto com água.
6) Verifique se os valores das etapas 4 e 5 coincidem ou se aproximam.
7) Compare e analise os resultados obtidos com cálculos e com medição.
Satisfação Garantida
Garantimos a sua nota e nos comprometemos em devolver o seu dinheiro caso não aprove o serviço prestado.
Análise Anti-Plágio
Antes da entrega, o seu trabalho passa por uma verificação Anti-Plágio para garantir a sua autenticidade.
Repeito aos Prazos
Asseguramos que o seu trabalho seja entregue no prazo acordado ou devolvemos o seu dinheiro.
Suporte Contínuo
Estamos sempre prontos para sanar todas as suas dúvidas, com suporte pré e pós compra via E-mail ou WhatsApp.
Equipe Qualificada
Contamos com uma equipe especializada e multidisciplinar pronta para atender a todas as suas demandas.
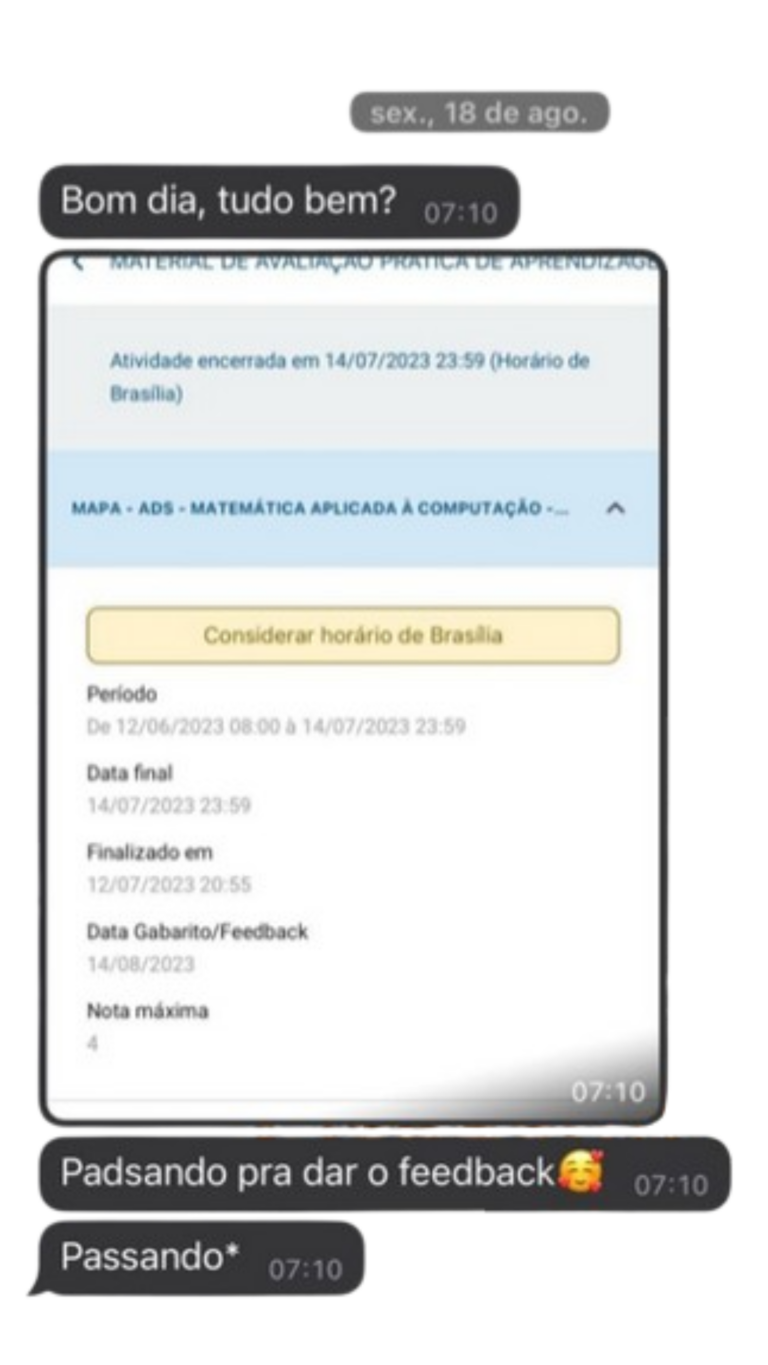
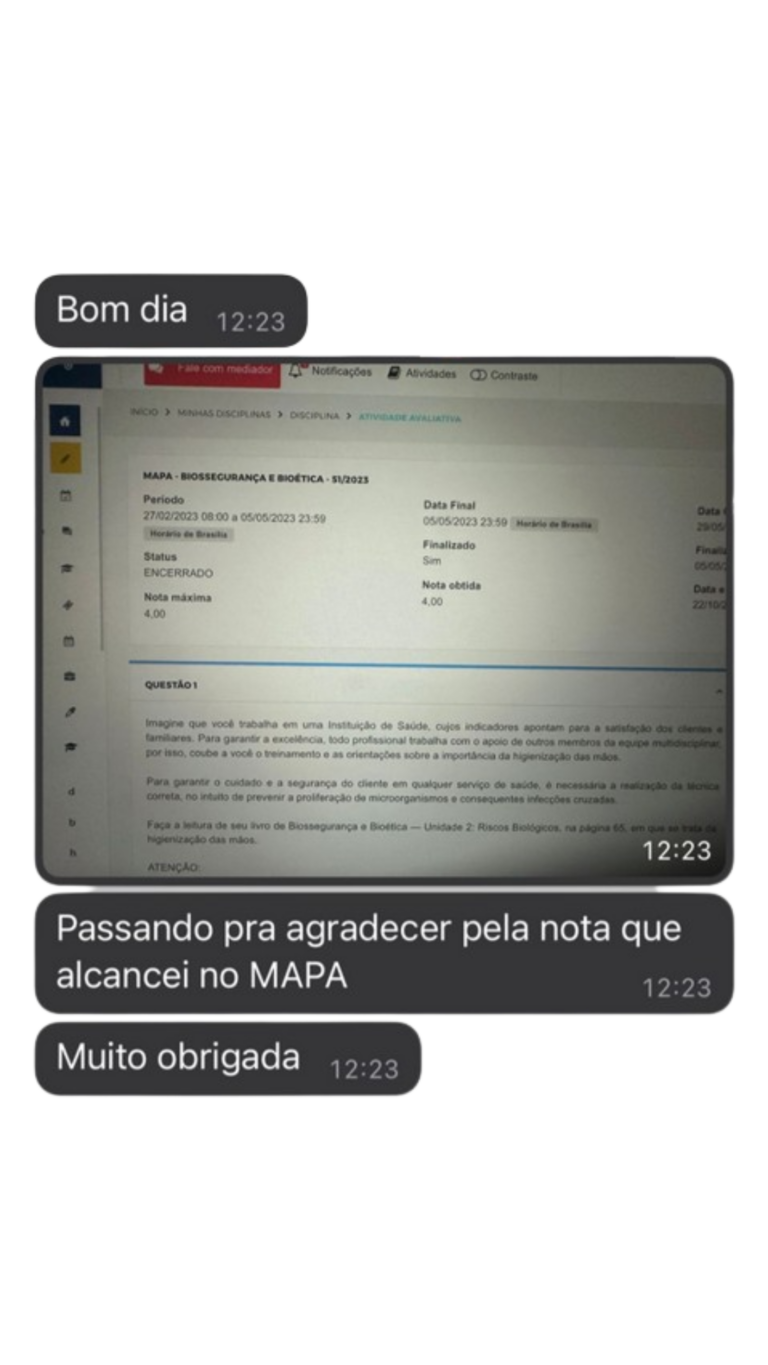
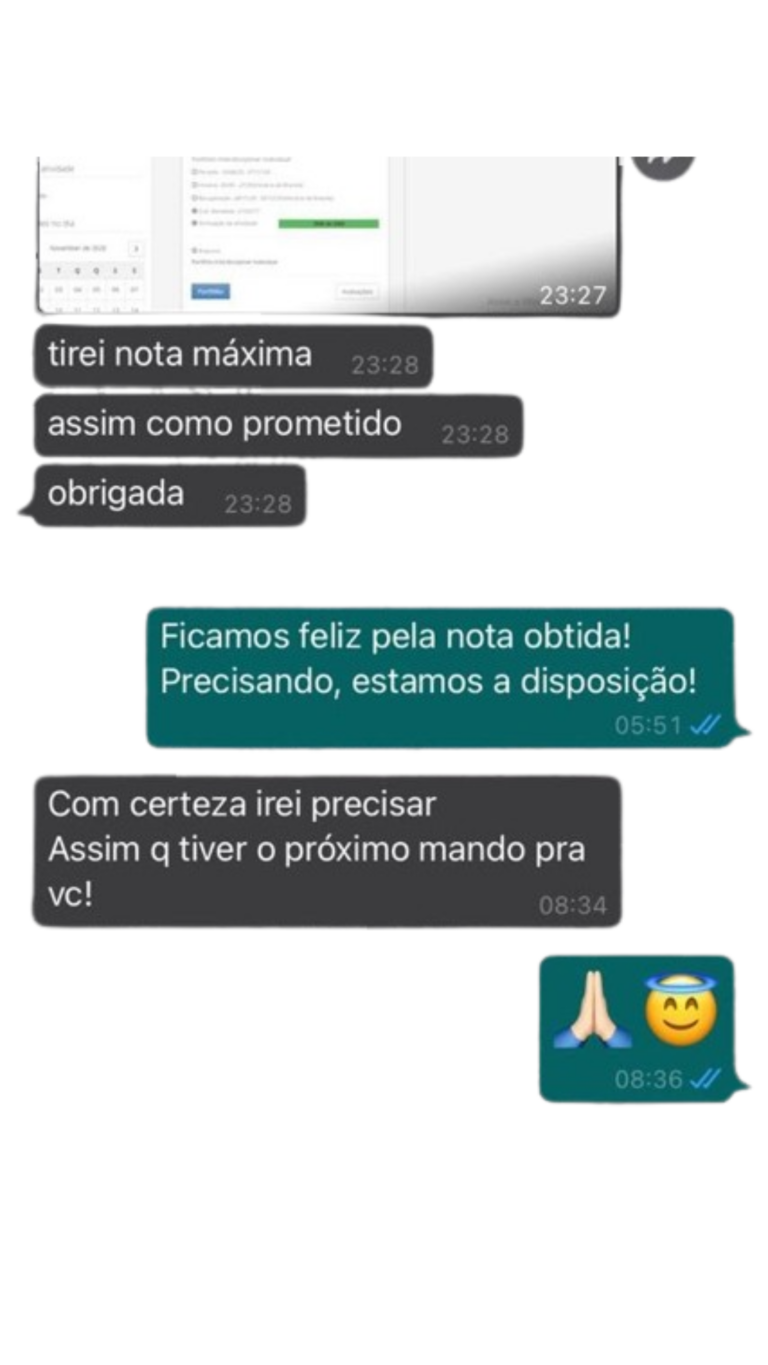
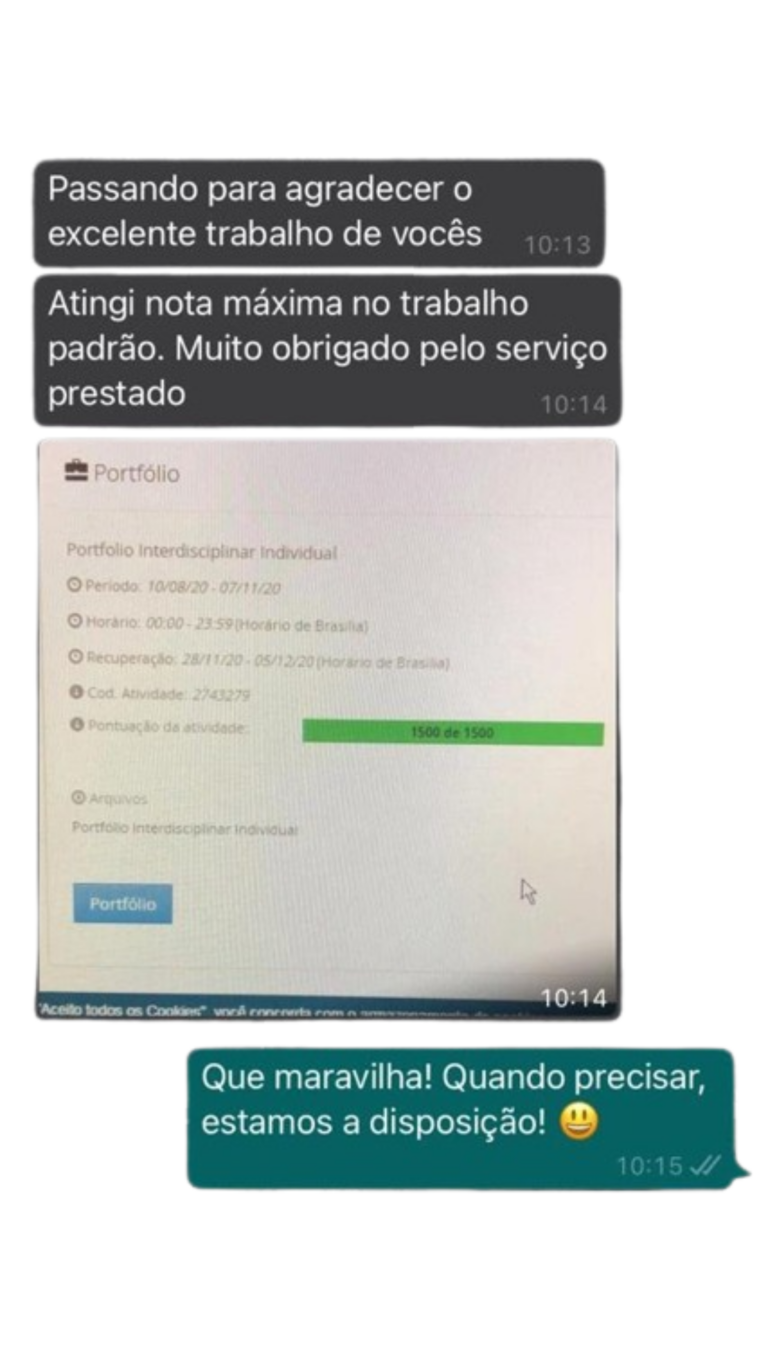







© 2024 | Nota 10 Acad | Todos os Direitos Reservados.